TEMA 5 FUNCIÓN DE PRODUCCIÓN NEOCLÁSICA

TEMA 5 FUNCIÓN DE PRODUCCIÓN NEOCLÁSICA

- febrero 19, 2018

TECNOLOGÍA

Proceso productivo + eficiencia técnica ... TECNOLOGÍA (Isocuantas)
Mapa isocuantas (representación gráfica)
Función de producción (representación analítica)
ISOCUANTA (definición): Lugar geométrico de todas las combinaciones de factores (procesos productivos) técnicamente eficientes que permiten obtener un determinado nivel de producto

PROCESO PRODUCTIVO: Combinación de factores que permite obtener un determinado output
EFICIENCIA TÉCNICA: No existe otro proceso productivo que utilice menos de algún factor y no más de otro para obtener el mismo nivel de producto
Si los procesos son perfectamente divisibles e independientes, sus combinaciones deben ser técnicamente eficientes AD isocuanta de X

Propiedades isocuantas

Cardinalidad: Cuanto más alejada del origen está una isocuanta, mayor es el nivel de producto X^0 < X^1 < X^2
Convexidad y estricta convexidad: Cualquier combinación lineal de dos procesos productivos permite obtener al menos el mismo nivel de producto, garantiza la eficiencia técnica
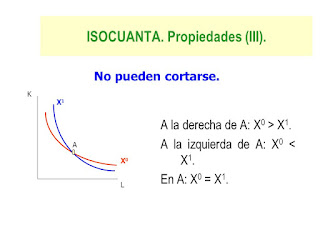
No pueden cortarse; a la derecha de A: X^0 > X^1, a la izquierda de A: X^0 < X^1, y en A: X^0 = X^1

Función de producción: máxima cantidad de producto con cada combinación eficiente de factores que se considere. Analíticamente X = F(K,L). Gráficamente: mapa de isocuantas
Relación Técnica de Sustitución

Cantidad que la empresa está dispuesta a sustituir de un factor (K) por el otro (L), manteniendo constante el nivel de producto RTS (L,K) = - dK/dL
Es la pendiente, en cada punto, de una isocuanta
La RTS decrece a medida que aumenta L y crece a medida que disminuye L
K ... O ... L
alfa\( Tg alfa = - dK/dL = RTS^A
RTS^C > RTS^A > RTS^B

Elasticidad de sustitución: variación porcentual de la relación K/L ante un cambio porcentual de la RTS

Alfa = [d(K,L)/dRTS] [RTS/(K/L)]

Función de producción a corto plazo, un factor fijo (K = K^0)

X = F (K^0, L) = f(L)
K ... K^0 ... O ... L^0 ... L^1 ... L^2 ... L
En K^0 línea horizontal y por L^=, L^1 y L^2 isocuantas
X ... X^2 ... X^1 ... X^0 ... O ... L^0 ... L^1 ... L^2 ... L
Uno origen, X^0 con L^0, X^1 con L^1 y X^2 con L^2 X = f(L)

Productividad media

Producto por unidad de factor variable
PM = X/L
Pendiente del rayo vector que sale del origen
X ... O (/ beta ... L
( cruza por arriba a /
Tangente beta = PM

Productividad marginal

Incremento del producto obtenido por la última unidad del factor variable
Pm = dX/dL
Pendiente del rayo vector en cada punto
X ... O (/ beta ... L
/( tangente (en punto corte alfa)
Tangente alfa = Pm

Ley de rendimientos decrecientes

A partir de un determinado nivel de utilización del factor variable, los sucesivos aumentos de la cantidad utilizada de éste, combinados con una cantidad constante del factor fijo, darán lugar a incrementos del producto cada vez menores.
X ... O ... L^0 ... L^1 ... L^2 ... L
Desde O levanto /
Desde L^0 y L^1 levanto | hasta / y uno origen con punto corte /| L^0 y L^1

Relación entre productividades

dPM/dL = d(X/L)/dL = [(dX/dL) - X/L]/L = [Pm - PM]/L
Pm > PM --> dPM/dL > 0
Pm = PM --> dPM/dL = 0 ÓPTIMO TÉCNICO
Pm < PM --> dPM/dL < 0

Tecnología a largo plazo, rendimientos de escala, cuánto varía el producto cuando se varía cantidad utilizada de los factores en la misma proporción X^0 = F(K^0, L^0) X^1 = F(人K^0, 人L^0)

Rendimientos crecientes de escala: el output crece más que proporcionalmente

X^1 > 人X^0

Rendimientos constantes de escala: el output crece proporcionalmente

X^1 = 人X^0

Rendimientos decrecientes de escala: el output crece menos que proporcionalmente

X^1 < 人X^0

Comentarios